
Published by K12 Handhelds, Inc.
Portal, AZ
www.k12handhelds.com
Copyright © 2006 by K12 Handhelds, Inc. License CC-by, 
This work is licensed under a Creative Commons Attribution 3.0 United States License.
Developed in conjunction with Monroe 2-Orleans BOCES.
Table of Contents
- Adding and Subtracting Simple Equations
- Multiplying and Dividing Simple Equations
- Two-Step Equations
- Adding and Subtracting with Multiple Terms
- Multiplying and Dividing More Complex Equations
- Factoring Trinomials
Adding and Subtracting Simple Equations
(monomials)
Algebra is a kind of math that uses letters to represent unknown numbers in equations. Our task then is to solve for the unknown. For example:
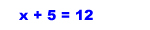
In this equation, x is the variable. It stands for some unknown number. We need to find the value of x.
To solve for x, our goal is to get x on one side of the equation all by itself.
To do this, we can follow the rules of math. We must keep the equation in balance. So whatever we do on one side of the equation, we must do to the other side as well.
To get x by itself, we use inverse operations to undo whatever is with x. This means, we do the opposite. If something is added to x in the equation, we need to subtract it to get rid of it. If something is subtracted from x, we need to add it to get rid of it.
In the equation x + 5 = 12, we need to undo the 5 by subtracting. We must subtract the 5 from both sides:

Our answer is x = 7.
For every equation you solve, you can check your work by substituting your answer back into the problem to see if it is correct. For example:
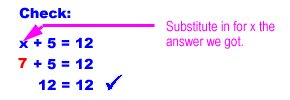
When we substitute in 7 for x, the equation is true, so we know we have the right answer. One nice thing about algebra is that you can always check and see if you got the right answer!
Let's look at a few more examples.

And let's check our answer of 21:

Here's another problem:
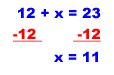
Let's check our answer of 11.

Now you try some. Solve for x for each of these. Don't forget to check your work (either on paper or mentally).
1. Solve for x: x - 3 = 10
2. Solve for x: x + 9 = 24
3. Solve for x: 7 + x = 15
Multiplying and Dividing Simple Equations
(monomials)
Another kind of algebra problem involves multiplication and division. Just as we learned before, we have to undo the math to get x by itself.
If x is multiplied by a number, we need to divide both sides by that number to get the answer. If x is divided by a number, we need to multiply both sides by that number to get the answer.
Here's an example:

To get x by itself, we need to divide both sides by 3.

Let's check our work.

Let's do a problem where x is divided by a number.
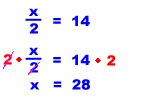
For this problem, we had to multiply by 2 to get x by itself. Let's check the answer:

Now work through some of these problems yourself. Make sure to check your work.
4. 
5. 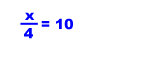
6. 
Two-Step Equations
Some algebra equations require more than one step to solve. Getting x by itself requires at least two steps. For example:
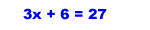
When you have both multiplication and addition, undo the addition first.
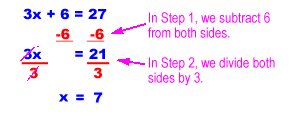
Let's check our answer of 7.

OK. Let's try another problem. Remember that when you have both multiplication (or division) and addition (or subtraction), undo the addition (or subtraction) first.

Don't forget to check your work. (You can get a perfect score every time if you do this and rework any problems that don't check out.)

Here's another example.

And the check:

You may want to review the rules for adding, subtracting, multiplying, and dividing negative numbers in the Integers ebook.
If you have a division problem where you are solving for x, you can also cross-multiply. Cross-multiplication looks like this:

Let's check our work:

Here's another cross-multiplication example:
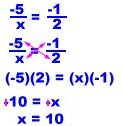
And the check of our work:

Now you try some of these. You can do your work with paper and pencil.
7. 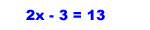
8. 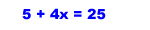
9. 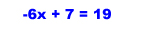
Adding and Subtracting with Multiple Terms
(polynomials)
When you are asked to simplify an expression, it means to combine any terms that can be combined. You can only combine algebra terms that have the same variable and exponent.
If the variable and the exponent are the same, you can combine terms by adding the coefficients. The coefficients are the numbers before the letters. For 2x, 2 is the coefficient.
For example, you can combine 2x + 3x to get 5x. However, you cannot combine the terms 3x + 4x2.
Here are some more examples.
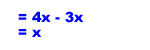
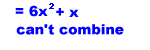
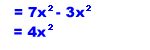
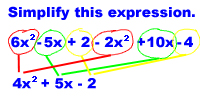
Let's look at simplifying some more complicated expressions. The first step is to find the terms that have the same variable and exponents. Then combine those.

As you work on these, don't forget the order of operations.
P - Parentheses
E - Exponents
M - Multiplication
D - Division
A - Addition
S - Subtraction
Let's do another example.
Simplify these expressions using paper and pencil and then choose the correct simplified answer.
10. Simplify 2x2 + 5x – 6
A) 7x2 – 6
B) 4x2
C) 2x2 + 5x – 6
D) 10x2 – 6
11. Simplify 3x2 + 6x + 7 + 2x2 + 2x + 3
A) 13x2 + 10
B) 6x2 + 12x + 21
C) 5x2 + 8x + 10
D) 5x2 + 12x + 21
12. Simplify 2x2 – x + 6 + 2x2 + x – 1
A) 2x2 + 5
B) 4x2 + 5
C) 4x2 + 2x + 5
D) 2x2 + 2x + 5
Multiplying and Dividing More Complex Equations
(monomials and binomials)
Now we're going to look at multiplying different algebraic expressions. Reviewing your PEMDAS order of operations will help with these problems.
Let's start with a simple example. (You can go to the ebook on exponents for a review.)

If we have a term outside of the parentheses, it must be multiplied by each term inside the parentheses. For example:

Let's do one with 3 terms.
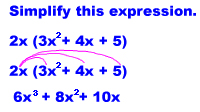
After doing each problem, make sure there is no further simplification that can be done. We can do this by seeing if there are any terms with like variables and exponents.
When multiplying two sets of terms in parentheses, we use a method called FOIL. FOIL tells you what to multiply.
F - first terms
O - outer terms
I - inner terms
L - last terms
It looks like this:
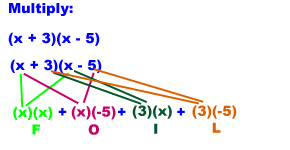
After we've applied FOIL, we need to multiply and simplify:

Let's do one more FOIL problem.
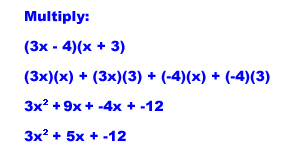
Now it's your turn to do some problems. Multiple each of these out on paper and then choose the correct answer to check if you are right.
13. Multiply (x + 4)(x – 8)
A) x2 + 4x + 32
B) 2x2 + -4x + -32
C) x2 + -4x + 32
D) x2 + -4x + -32
14. Multiply (x – 5)(2x + 1)
A) 2x2 + 9x + -5
B) 2x2 + -11x + 5
C) x2 + -9x + -5
D) 2x2 + -9x + -5
15. Multiply (x – 10)(x + 5)
A) x2 + -10x + -50
B) x2 + -5x + 10
C) x2 + -5x + -10
D) x2 + -5x + -50
Now let's look at dividing.
When you divide multiple terms by a single term, you must divide each of the top terms by the bottom one. You then simplify and reduce.
Here is an example:

When you divide terms with the same variable, you can cancel the variables. If the exponents are different, cancel by subtracting the exponents. (Review the ebook on exponents for more information on this.)
Here's another example:
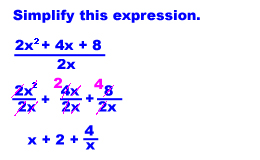
Now, you do a few. Simplify these expressions by working them out on paper and then choose the correct answer.
16. 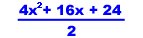
A) 2x2 + 8x + 12
B) x2 + 8x + 12
C) x2 + 8x + 12
D) 22x2
17. 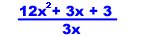
A) 4x2 + 2 + 12
B) 4x + 1 + 1/x
C) 4x + 2
D) 4x2 + 1 + 1/x
Factoring Trinomials
Now we're going to learn about factoring trinomial expressions. (Trinomials are algebra expressions with 3 terms.) This is the opposite of FOIL. For an expression such as:
x2 + 3x + 2
We need to figure out the factors. (?? + ??)(?? + ??)
We need to do some intelligent guessing like a detective to solve this. We can use what we know about FOIL to solve this.

We know from FOIL that the first term times the first term is x2, so the first terms must be x.
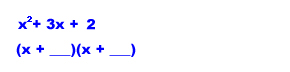
According to FOIL, we know that the last two numbers must multiply to equal 2. To find these terms, we can look at the factors. Don't forget negative numbers!
The number 2 only has two sets factors (1 • 2 and -1 • -2).
Let's try both sets to see which gives us the right middle term.

This looks like the right answer! Let's check -1 and -2 just to double-check.
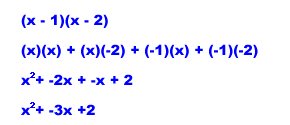
This is not the correct answer. Our first answer (x + 2)(x + 1) is correct.
We can use FOIL to check our answer:

Let's do one more.

Now we have to find the factors of -4. They are:
-2 • 2
-4 • 1
-1 • 4
Let's try one at a time and see which one works.
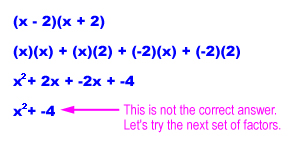
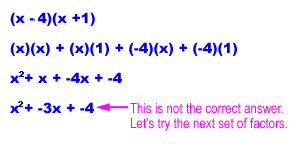
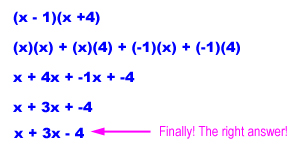
Now it's your turn. Factor these expressions using the method we just learned.
18. Factor x2 + 5x + 6
A) (x – 3)(x – 2)
B) (x + 1)(x + 6)
C) (x – 1)(x – 6)
D) (x + 3)(x + 2)
19. Factor x2 + 2x + -8
A) (x + 1)(x – 8)
B) (x – 1)(x + 8)
C) (x – 4)(x + 2)
D) (x + 4)(x – 2)